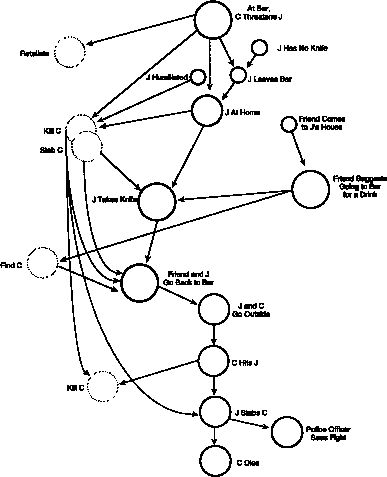
Figure 2. Causal event chain given by Juror 128
While presenting such an integrated theory is beyond the scope of this presentation, it is possible to demonstrate that these two approaches are both consistent and complementary. This will be made clear by presenting TEC-ECHO simulations of some of the data which has been used to support the Story Model. To understand these examples, the two frameworks will first be described and then the simulations presented. A discussion of the implications for both approaches and possible integration will follow the presentation of the simulation models.
In TEC, "explain" is taken to be a primitive relation between propositions (P, Q, and P1..Pn) in an explanatory scheme (S). Coherence, then, is the extent to which the propositions in the system follow the "principles" of explanatory coherence:
Principle 1. Symmetry
(a) If P and Q cohere, then Q and P cohere.
(b) If P and Q incohere, then Q and P incohere.
Principle 2. Explanation
If P1...Pm explain Q, then
(a) For each Pi in P1...Pm, Pi and Q cohere.
(b) For each Pi and Pj in P1...Pm, Pi and Pj cohere.
(c) In (a) and (b) the degree of coherence is inversely proportional to
the number of propositions P1...Pm.
Principle 3. Analogy
If P1 explains Q1, P2 explains Q2, P1 is analogous to P2, and Q1 is
analogous to Q2, then P1 and P2 cohere, and Q1 and Q2 cohere.
Principle 4. Data Priority
Propositions that describe the results of observations have a degree of
acceptability on their own.
Principle 5. Contradiction
If P contradicts Q, then P and Q incohere.
Principle 6. Competition
If P and Q both explain a proposition Pi, and if P and Q are not
explanatorily connected, then P and Q incohere. Here P and Q are
explanatorily connected if any of the following conditions holds:
(a) P is part of the explanation of Q.
(b) Q is part of the explanation of P.
(c) P and Q are together part of the explanation of some proposition, Pj.
Principle 7. Acceptability
(a) The acceptability of a proposition P in a system S depends on its
coherence with the propositions in S.
(b) If many results of relevant experimental observations are
unexplained, then the acceptability of a proposition P that explains
only a few of them is reduced.
which were taken directly from Thagard (1992a). The coherence of a large system of explaining and contradicting propositions cannot be computed simply by informally applying the principles of TEC (despite criticisms to the contrary, which have not demonstrated themselves to be successful). In light of this, a connectionist (though not PDP) system called ECHO has been developed which makes this computation straightforward. TEC and ECHO have been used to explain numerous scientific revolutions such as the Copernican revolution (Nowak & Thagard, 1992; Thagard, 1992a) as well as various complex decisions, such as Hitler's belief the Allies would invade Calais rather than Normandy and the decision of the captain of the USS Vincennes which led to the destruction of a passenger aircraft (Thagard, 1992b). Most closely related to the present issue, ECHO has been used to model prominent jury verdicts (Thagard, 1989), though this work did no tmodel the decisions of individual jurors, nor were the ECHO models based on explanations actually provided by human subjects.
One of the criticisms that has been raised (e.g. Giere, 1993) about the ECHO simulations is that the "explanations" have been provided to the system by the programmer--that is, the propositions used and the explanatory and contradictory links between them have all been decided upon by the same person, and since it is impossible to know what explanations that, say, Darwin actually considered, the simulations are in some way invalid.(1) The simulations presented here later address this issue by using the explanations provided by the jurors themselves rather than explanations provided by the programmer.(2)
(1) Story Construction, "an active, constructive comprehension process in which they make sense of trial information by attempting to organize it into a coherent mental representation" (Pennington & Hastie, 1992, p. 190). These representations typically take the form of stories with causal links between episodes in the story. It is possible for jurors to construct more than one story, and in that case stories are judged on the basis of their acceptability. According to the Story Model, acceptability is a function of coherence, completeness, and uniqueness. These principles, when explained in greater detail, parallel those of TEC, as has been observed both by Thagard (1989) and Pennington and Hastie (1993).
(2) Verdict Representation, in which the juror constructs a representation of the possible verdicts. In most criminal cases, verdicts consist of more than simply "guilty" or "not guilty." For example, in the murder case used in Pennington and Hastie (1986), the jurors have four options: first-degree murder, second-degree murder, manslaughter, and not guilty. Verdicts are represented along four axes: identity (i.e. was the defendant the one?), mental state of the defendant at the time, circumstances during the event, and the actions taken by the defendant. While jurors differ from one another in terms of their representations of the verdicts, this does not play a central role, as differences in verdict representations are not associated with differences in decision outcomes (Pennington & Hastie, 1986).
(3) Story Classification, in which the story constructed in step 1 is matched to the verdicts represented in step 2. The central element here is the goodness of fit between the story and the various verdicts. The verdict with the best fit to the story is hypothesized to be the one chosen by the juror.
The relationship between the Story Model and ECHO is clear: ECHO provides a computational account of the acceptability of the stories constructed and the story classification processes, and, to the extent that juror's decisions are in accord with ECHO predictions, supports the psychological plausibility of ECHO. To demonstrate this more conclusively, I constructed ECHO simulation models based on the causal stories of two of Pennington and Hastie's (1993) subjects. These ECHO models do indeed reach the verdicts that the subjects reached, and have other interesting properties.
Figures 1 and 2 are reproductions of the Pennington and Hastie's (1993) Figures 3 and 4 (pp. 144, 145), which represent the stories generated by Juror 109 and 128, respectively. In these figures, [e]vents and episodes are represented by solid circles and the diameters of the circles indicate the degree of elaboration provided of events by the jurors; broken circles represent the defendant's goals, inferred by the juror. The arrows connect events that were explicitly linked by causal relations in the juror's verbal report. The letters J and C refer to the defendant Johnson and the victim Caldwell respectively.
It is important to note that Juror 109 delivered a "not guilty" verdict and Juror 128 delivered a "first-degree murder" verdict, after both of them had seen exactly the same evidence presented in exactly the same manner. The clear difference between the two jurors was in the stories they generated to explain the events which led to the trial.
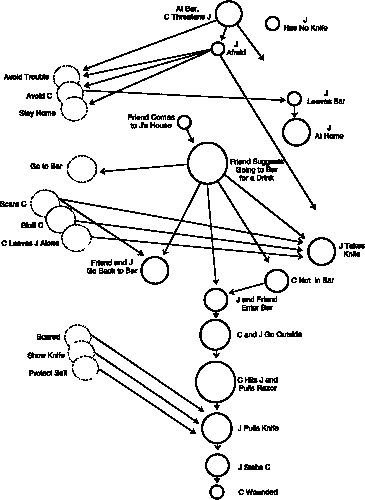

Figure 2. Causal event chain given by Juror 128
The four possible final verdicts generated four propositions. Since those verdicts are generally exclusive, five contradictory links were generated between pairs of final verdicts. The final verdict delivered by the juror was assumed to be the final verdict proposition with the highest activation at the end of the ECHO run, since ECHO activation level is intended to correspond to belief strength. Nineteen propositions were generated by the testimony itself; while there were certainly more than 19 propositions in the testimony, those that seemed the most directly relevant were used. There were several pieces of directly contradictory testimony and these were included to see how ECHO would handle the contradictions.
Since one of the aims of this paper was to remove the supposed "programmer bias," and the stories of the two jurors included few references to the actual evidence, there were two models made for each juror: one including the testimony propositions and one without the testimony, as it is not guaranteed that the links made from the evidence to the story are exactly the ones made by the jurors. While this does have some impact on the ECHO network as a whole, the impact on the final decisions was negligible.
Juror 109's story consisted of 26 propositions and 18 explanations, all of which were again derived from the causal graph (Figure 1). Nodes from Figure 1 were represented in ECHO by propositions and links in the graph by ECHO explanations. Seven explanations/contradictions connected Juror 109's story to the verdict categories, and 19 more were necessary to connect the story to the testimony.
The story for Juror 128 consisted of 19 propositions and 14 explanations, all of which were derived directly from the graph presented in Figure 2 just as they were derived from Figure 1 for Juror 109. Eight explanations/contradictions connected Juror 128's story to the verdict category propositions. It should be noted that one of the propositions in Juror 128's story actually was a piece of the testimony, so only 18 additional explanations or contradictions had to be added to link the story to the 19 testimony propositions.
There are a several things to note about the simulation results. First and foremost, the simulations are in agreement with the verdicts reached by the jurors that were modeled. Second, according to ECHO, both of the stories constructed by the jurors are coherent explanations. This is important in that the explanations used were those constructed by the jurors themselves and not the ECHO programmer. Third, both explanations become even more coherent when related to the testimony. This is particularly interesting since the two stories yield opposing verdicts, and the testimony presented is not itself consistent. Both stories formed by the jurors integrate this contradictory testimony in a coherent way, even though the stories themselves differ dramatically.
| Juror 109 | Juror 128 | ||||
|---|---|---|---|---|---|
| story only | with testimony | story only | with testimony | ||
| Total coherence | .37 | .59 | .49 | .78 | |
| Not guilty by self-defense | .34 | .40 | -.54 | -.54 | |
| Manslaughter | -.47 | -.40 | -.26 | -.28 | |
| Second-degree murder | .10 | -.09 | .49 | .49 | |
| First-degree murder | .12 | .03 | .56 | .57 | |
Another interesting facet of the ECHO models relates to the testimony. Since the jurors did not observe any of the events as they happened, they must rely on the testimony and their own inferences to guide them. In many legal cases, though, testimony is somewhat less than guaranteed to be an accurate description of the events that took place. In the case examined by these jurors, the defendant and one of his best friends are also witnesses. Are they to be believed? As it turns out, whether or not the witnesses are believed depends on the content of their testimony. According to the ECHO simulations, testimony will be believed to the extent that it is coherent with the story that the juror constructs. In these simulations, for example, almost all of the defendant's testimony ends up with negative activation values (is not believed) for Juror 128, and all of it ends up with positive activation values for Juror 109. This is consistent with many of the ECHO simulations of scientist's beliefs, wherein certain experiments are considered "anomalies" and not believed by the scientists.
Second, the Story Model has been applied primarily to the domain of juror decisions. While, in principle, the Story Model is part of a more general framework of explanation-based decision making, most of the work on explanation-based decision making has been conducted as work on the Story Model. While this is certainly reasonable given the complexity of the task confronting jurors, the success of ECHO in domains outside of juror decision bodes well for the extension of the Story Model to other domains.
The support for ECHO would be stronger if the stories that individual jurors rejected were also included and shown to have lower coherence than the story each juror decided upon. Another point in support would be if two jurors with contradictory stories were brought together and the juror with the story having greater total coherence "won" out (Juror 128 in this case). In fact, such an enterprise would be quite useful, extending both the Story Model and ECHO to the domain of complex decision-making by groups and not just individuals.
Glymour's second criticism is addressed by this work as well. Glymour's "pocket calculator" algorithm (1992, p. 474) for ECHO has a critically linear aspect to it which is not found in ECHO. While it may indeed agree with ECHO that the jurors' stories are coherent and yield the decisions they do, it is unclear that Glymour's algorithm will yield increases in coherence for both stories given the inconsistent nature of the testimony. Again, until Glymour can demonstrate a simpler algorithm that yields the consistency of results that ECHO does, there is no reason to believe that Glymour's criticism is a valid one.
What Is an Explanation? One of the criticism that has been leveled at TEC-ECHO by both the previously-mentioned critics (Giere, 1993; Glymour, 1992) is that ECHO begs the question of what an explanation is. When "P explains Q" is provided in the context of TEC, what does "explain" actually mean? Are all explanations the same? Thagard (1992a) attempts to address this question with the answer that explanations take a variety of forms. Explanation, Thagard maintains, is a complex process that can include suprocesses based on deductive, statistical, schematic, analogical, causal, or linguistic/pragmatic subprocesses. There is no single way to construct an explanation, and the "goodness" of an explanation is a function of the explanatory system in which it is embedded.
This is entirely consistent with the data provided in Pennington and Hastie (1993). The inferences which connect one part of their story with the next take a variety of forms, all of which are equally valid for that juror. In fact, several of the explanatory links shown in Figures 1 and 2 are broken down by Pennington and Hastie (1993) to more primitive inferences, each of which could also be analyzed with ECHO (e.g. Pennington & Hastie's (1993) Figures 5 and 6). Thus, there is no single answer to what an explanation is across all individuals, but once the (local) explanations have been formed, a given system of explanations seems to match the predictions made by TEC-ECHO. While this may be something of a difficulty for ECHO as a normative model, it provides healthy support for ECHO as a predictive one.
(2) It should also be noted that Thagard (1992a, Chapter 4) directly addresses this criticism in several different ways.
(3) Thagard (1992c) addresses this latter criticism quite effectively, this work merely serves to provide further evidence in favor of ECHO's algorithm.